机器学习算法中的数学思想

一、 机器学习的过程是在学习什么

以MNIST手写数字识别为例 MNIST是一个手写数字数据库，它是以一个28*28像素的图片以及一个对应的数字标签作为键值对的数据库。

为了更好的将这个识别过程数学化，先将输入的图形像素化，每一个数字图形可以按照各像素的明度值 转化为一个784个参数的列向量。
[0.1,0.3,0.4 ...... 0.0,0.8]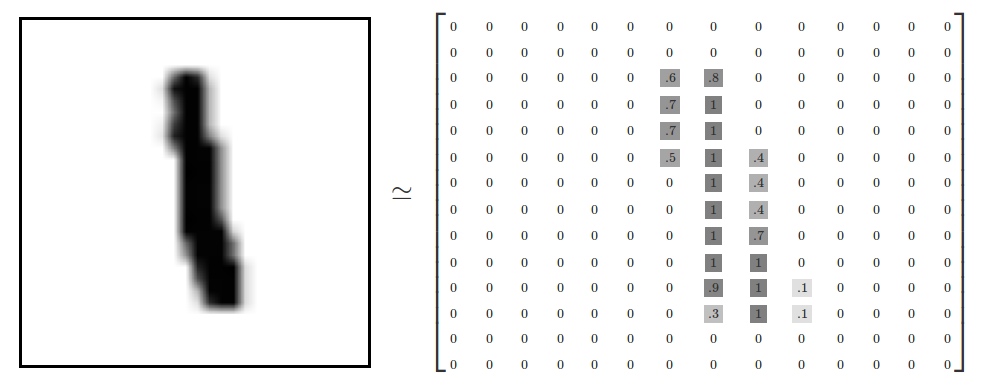

其中每个向量值代表一个像素对应的明度值。
假设学习模型为一个有两个隐藏层的全连接层。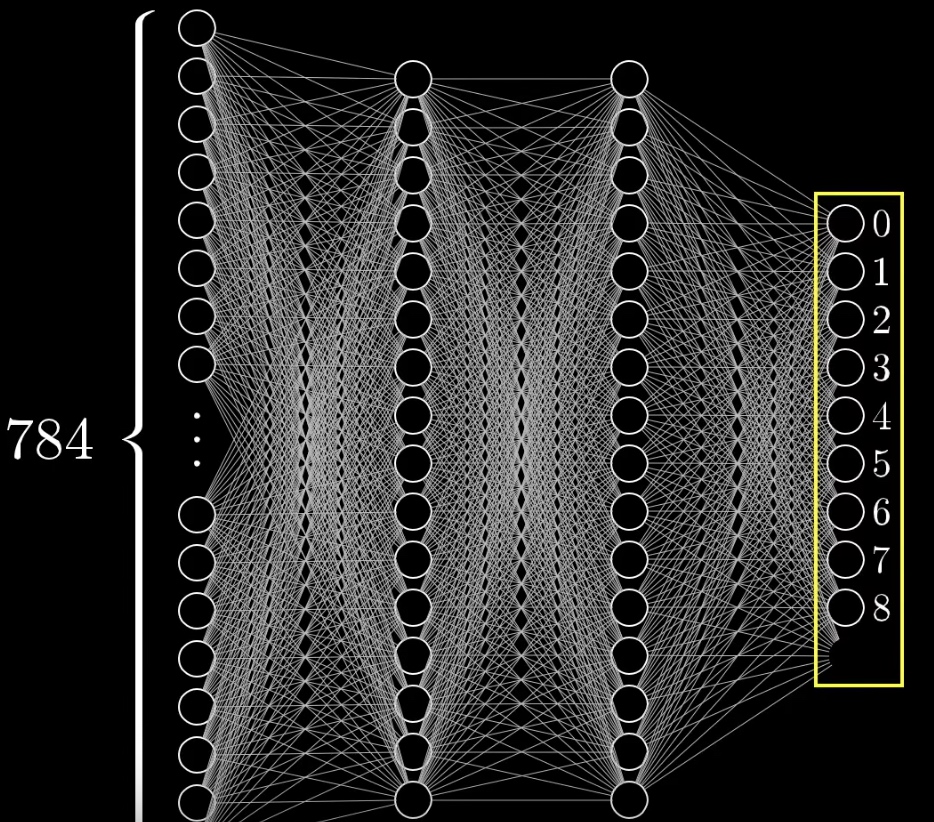

可以看到 每个神经元与神经元之间都由一根线连接着，这根线其实指代的是两个神经元之间的关系，用数学方式来说，可以称之为 权重值。

我们希望找到每根线所代表的权重，当输入一个手写数字图片的时候，通过第一层的权重值，点亮部分第一个隐藏层的神经元【注1】

注释1： 可以假设 最后一层隐藏的神经元所代表的是类似人类识别数字那样，指代组成数字的一些笔画，比如说圆圈或者竖线，那么第一层隐藏的神经元可能指代的是 组成哪些笔画的更细微一些的笔画，比如一个左上角的圆弧，一个左下角的圆弧之类，但其实机器学习的过程并非我们想象的那样，每一层代表的可能是一些我们人类都看不懂的信息，我们称之为features，或者说是特征。为了更好理解机器学习的数学原理，我们暂且这么认为。

那么 拿最后输出层的一个神经元 a2 来说，它就等于上一层神经元与权重值的求和$sum = \sum_j W_{i,j}x_j$
但只求和是不行的，因为对于输出端 a2来说，它的值必须在[0,1]范围内，这里就要用到sigmoid() 压缩函数。【注2】

注2： sigmoid 函数 是一个压缩函数 $ S(x) = \frac{1}{1+e_{-x}}$，sigmoid函数连续，光滑，严格单调，以(0,0.5)中心对称，是一个非常良好的阈值函数。
当x趋近负无穷时，y趋近于0；趋近于正无穷时，y趋近于1；x=0时，y=0.5。当然，在x超出[-6,6]的范围后，函数值基本上没有变化，值非常接近，在应用中一般不考虑。 在机器学习中，常常使用sigmoid函数 将相似率控制在0-1 范围内。

当然，神经元的触发难易程度也不应该是一样的，我们在求和函数$sum = \sum_j W_{i,j}x_j$中
增加一个偏置值$ b_i$，用来控制神经元激活的难易程度。
$sum = \sum_j W_{i,j}x_j+b_i$
那么 输出结果ai 就可以用公式表示为
$ a_i = sigmoid（\sum{w^{i-1}_j a_j^{l-1}+b_i}）$
所谓机器学习，就是找到上述有着无比复杂参数（偏置b和权重w）的函数funa（），求出其正确的偏置和权重值,使得我们每次输入一个手写图片向量，该函数都能在最后点亮输出向量中的某个神经节点。
所以： 机器学习的核心，就是使用合适的方法 去找到学习的数学模型里，所有的 偏置和 权重

反向传播

这是机器学习的核心，就是找到一个合适的方法，去调整偏置和权重，使输出层的结果尽可能的与我们期望的结果一致。
就以前面说到的识别mnist手写数字识别算法为例。
当输入一个手写数字 2 的时候

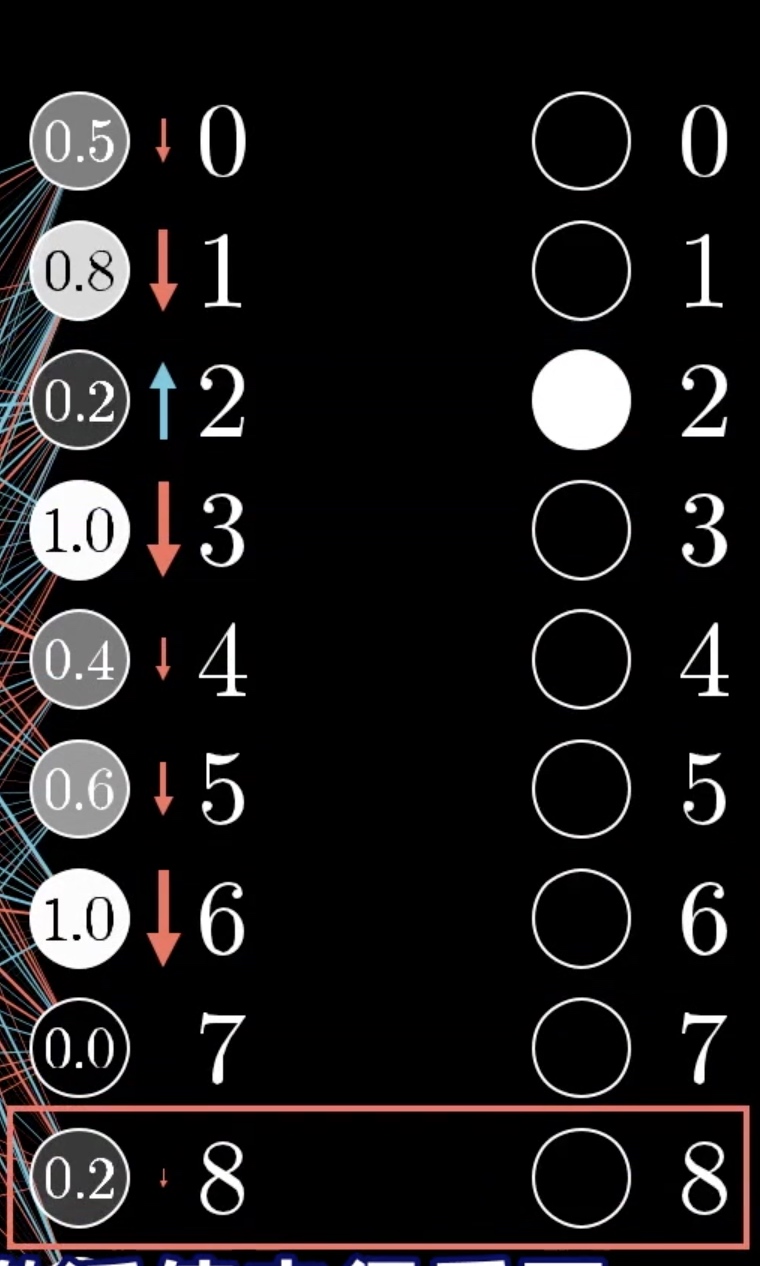
当模型还未完全训练完毕，输入的结果和输出的结果看起来应该是没有什么关联的。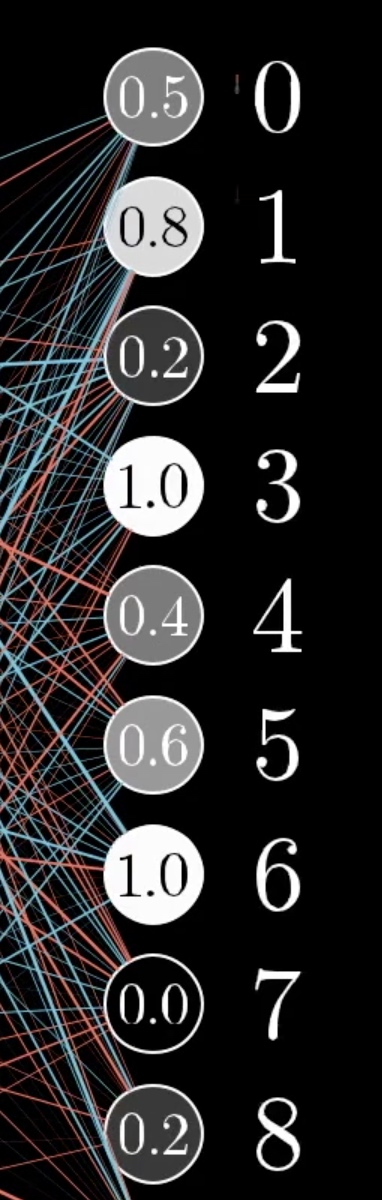

可以看到，尚未完成训练的模型，它的识别结果是很混乱的，同时点亮了好几个数字。

我们的期望： 是让数字2 对应的节点 值变得更大，让其他的节点 对应的结果值变得更小。同时 该变化应该和节点当前对应的值与期望值的差距成正比。

比如说 节点2 当前激活的值为0.2 我们期望的值是1，那么节点2变大 对于我们预测模型来说就比让节点8变为0要来的更重要，因为节点8 当前的数值0.2 已经和我们期望的0 差距不大了，而2对应的0.2 与我们当前期望的1差距显然要更大。
见下图：

我们知道，数字2 对应的值0.2 是将输入的748列向量的值，与对应的偏置和权重相乘之后求和，再通过sigmoid()函数 将其结果约束在[0,1]之间的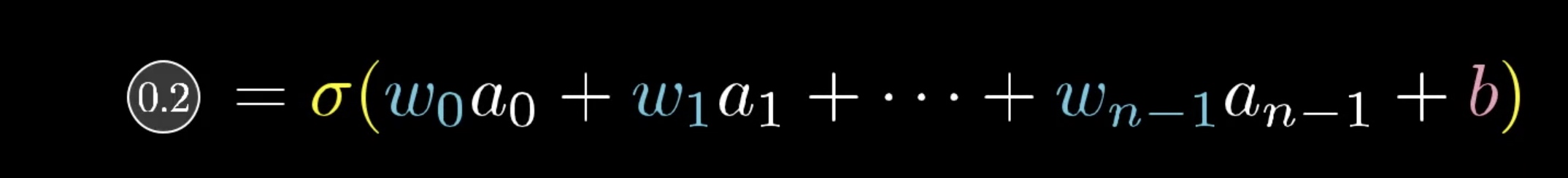

注： w0 w1 w2…. 为上一层（该例子中为第二个隐藏层）对应的每个神经元的权重，b为偏置向量。
如果要让0.2（即节点2对应的输出）变大，有三个途径

1. 增大权重wi
2. 增大偏置b
3. 修改ai的值

我们目前只关注如何修改权重 使得输出节点2 对应的结果变大。

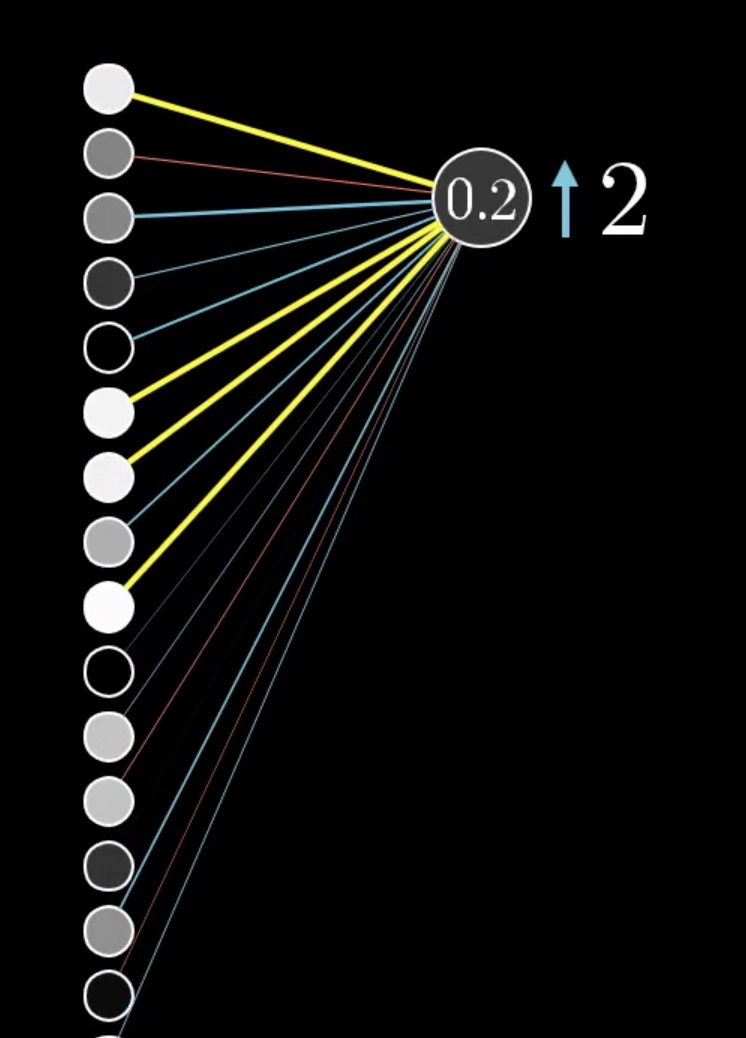
可以看到上一个链接层对应的激活情况如图。
如果我们要更改权重值， 那么1，6，7，9对应的神经节点的参数更改会更有意义，因为预测结果是上层神经元与权重乘积求和的，因为1678 对应的节点更亮，那么增大他们之间的权重值会更有意义。同样，如果如果我们更改节点的值，那么1，6，7，9对应的节点更应该增大，但现在我们无法更改节点值，只能通过更改权重和偏置的值来修改最终的计算结果。

这只是当只有一个输入的时候，输出结果告诉我们它对上个节点权重值变化的诉求，以这个例子为例，就代表
当输入一个手写数字2 的时候，为了使输出结果更接近为2，结果神经元要求上一个隐藏层中 第 1，6，7，9对应的节点的权重应该更大，那么当吧全部训练数据输入进来的时候，所有的输出结果对上一个神经元 权重的诉求就都可以获取到了，那么将全部的诉求求和求均，就得到整个样本对该模型 第二个隐藏层 权重变化的诉求。

损失函数

当学习模型尚未训练好，它给出的结果可以说是相当随机的，那么有必要告诉模型，当前的输出结果与预期结果偏差有多大。 这里便引申出损失函数的概念。

损失函数（loss function）是用来估量模型的预测值f(x)与真实值Y不一致的程度，它是一个非负实数值函数，通常使用L(Y,f(x))来表示，损失函数越小，模型稳健性越好。

在机器学习里 我们的损失函数一般是 预测结果和期望结果的平方差之和。
我们训练模型，就是为了是损失函数最小。
机器学习的损失函数可以表示为【注3】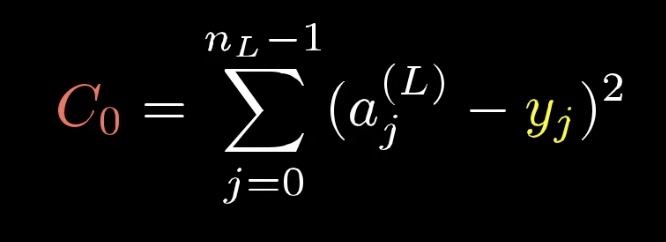

参数解释：
$a^j$：机器学习预测出的结果值
$b^j$： 目标期望值
$C_0$： 表示输入一个样本的损失值

其中 $a^j$ 又可以表示 上一层神经元与权重和偏置的加权和，我们记为z，对z进行sigmoid压缩得到的结果。

用公式可以表述如下：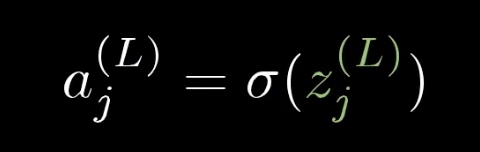

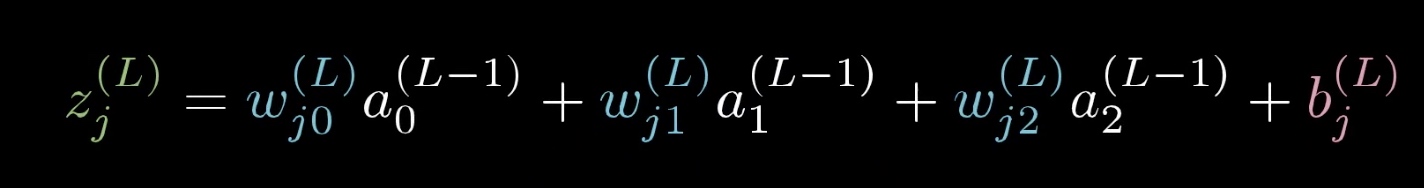
那么 可以看到 最终的损失值$C_0$ 可以表示为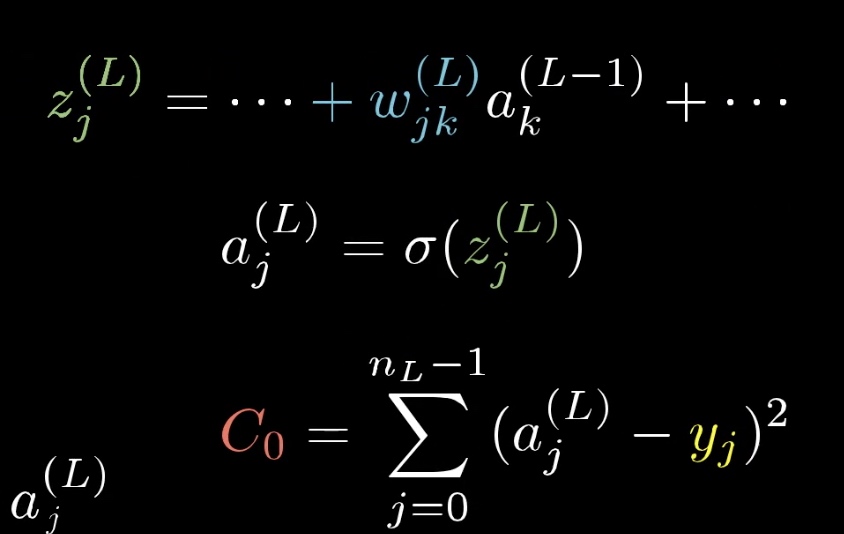

反向传播算法

正向传播过程

当我们输入随机的一组权重和偏置，以及一张手写数字数组之后，将其按照求和公式求和，可得到一组预测值。
这叫正向传播

正向传播： 根据输入的一组数据，计算出输出值

反向传播

概念： 当计算出预测值之后，因为它必定跟我们的期望结果有偏差，所以就需要将偏差值计算出来，将偏差反向传播，计算每个权重的偏导值，然后以一定的步长更新权重，减小误差，这叫反向传播。

上面说过，我们判断上个神经元层与输出结果的神经元之间的权重变化，他们不仅与当前计算结果和预期结果的偏差相关（表现在数学上，就是输出向量与预期向量$y = [0,0,1,0,0,0,0,0,0]$ 之间的求和平均数），还与当前神经元的数值相关。

对于上文中 我们说过的损失函数C，机器学习的目的就是通过改变对应的偏置b和权重w 使该函数最小，那么我们只需要求出 损失函数对每一个偏置和每一个权重的偏导数即可，知道了偏导数，我们就知道权重应该以什么样的方式，以多大的数量，增加还是减少，来影响最终的预测结果从而是损失函数降低到最小。一般的处理是，算出权重的梯度值之后，如果梯度为正，就意味着这里涉及到梯度下降算法的一些知识，可以详细的看一下梯度下降的维基百科，讲的很好

剩下的就是求偏导数的知识了，$C_0$ 对$ w_{l}^j$ 的敏感度，也就是偏导数，根据链式法则，可以求得为：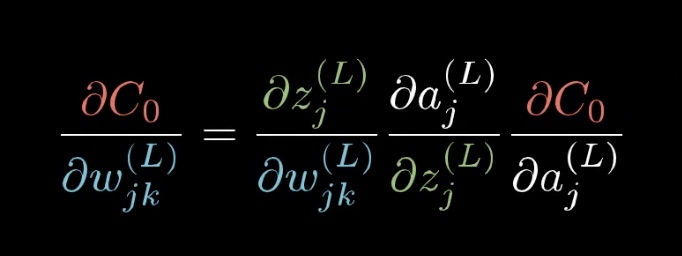

其中 每一项，抛去数学含义，它都是代表了一定意义的

1. $C_0$ 对$a_j^{L}$ 的偏导数： 因为平方差函数（损失函数c0）的偏导数斜率一般为正，所以该函数意味着 目标函数与预测函数之间的差距越大，偏置w的改变对该偏差值的影响就越大，与上文所讲的吻合，就是预测值和期望值之间的差距，也会对权重的改变产生影响。偏差越大的，他们的权重改变对偏差值的影响会更大。（就是改变这些偏差大的神经元他们链接的权重会更有性价比一些）
2. a对z求导：就是你所选的非线性激活函数对z的偏导数
3. $z^{L}j$对$w{jk}^{L}$ 的偏导数： 偏导结果其实是$f(a^{L-1})$ ，意味着 L层的权重$w^{L}_{jk}$ 对偏差值的影响 受到它上一层的神经元的影响。也就是一同激活的神经元联系在一起这句话的由来

说到这里，我们有必要看一下 $C_0$ 对$a_j^{L-1}$（L1层的神经元）的敏偏导数。这是理解反向传播算法的核心
虽然上文说过 我们无法改变$a_{L-1}$层神经元的值，只能改变他们的权重和偏置，但是看一下

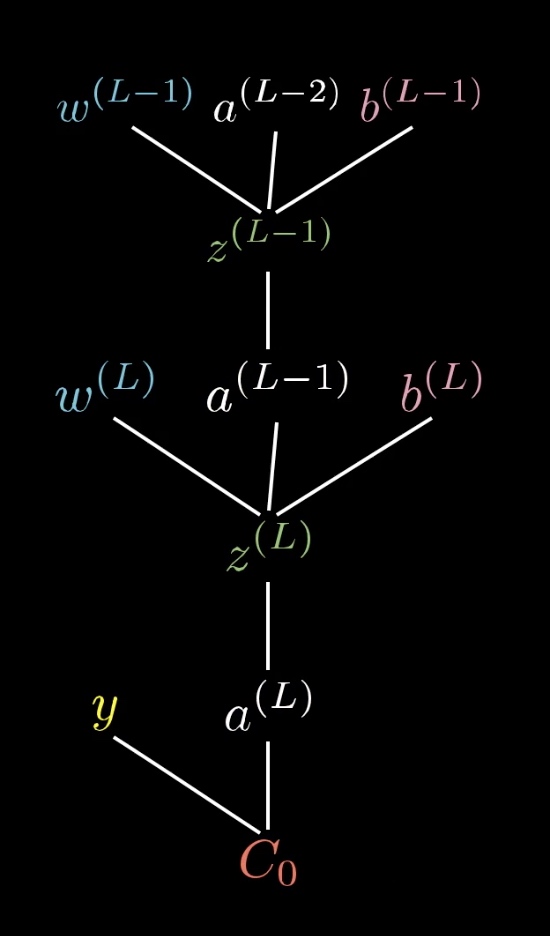
$a^(L-1)$ 与$z^{L-1}$ 、$w^{L-1}$、$a^{L-2}$ 、$b^{L-1}$是直接相关联的，那么如果知道
$C_0$ 对$a_j^{L-1}$的偏导数，那么反过来用求导公式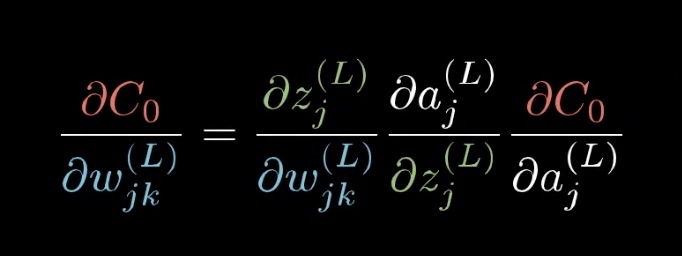

（将公式中的L 替换为L-1，同时左边的移动到右边，也就知道了代价函数对之前偏置和权重的偏导数了。
对上一层神经元的的偏导数：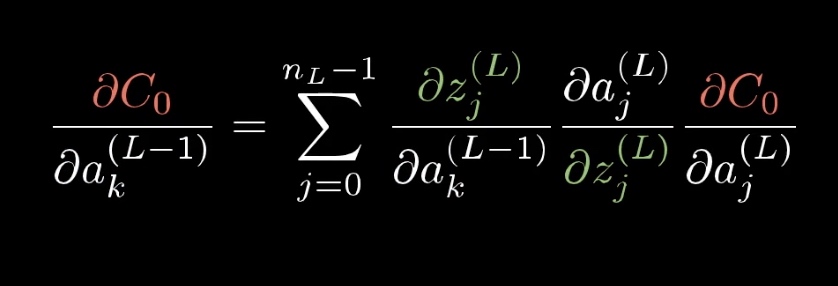

这里也可以看出，上一层神经元对代价函数的影响是同时通过下一层神经元的共同作用而影响的（因为偏导数是下一层神经元的偏导数乘积之和 ）

将上式展开，可得偏差函数对L层每一个权重的偏导数为：

当求出$w_jk^{(L)}$的偏导数，下一步只需要采用合适的最优化方法，更新该偏导数的值，就可以使误差逐步减小。

关于反向传播算法的具体例子，可以参考这篇博客，以具体的例子展示了反向传播的过程中 权重值是如何变化的。